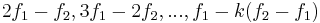Combination tone

A combination tone, also called a sum tone or a difference tone (also occasionally resultant tone), can be any of at least three similar psychoacoustic phenomena. When two tones are played simultaneously, a listener can sometimes perceive an additional tone whose frequency is a sum or difference of the two frequencies. The discovery of some of these phenomena is credited to the violinist Giuseppe Tartini, and so the tones are also called Tartini tones.

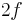One way a difference tone can be heard is when two tones with fairly complete sets of harmonics make a just fifth. This can be explained as an example of the missing fundamental phenomenon.[1] If f is the missing fundamental frequency, then 2f would be the frequency of the lower tone, and its harmonics would be 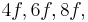4f, 6f, 8f, etc. Since a fifth corresponds to a frequency ratio of 2:3, the higher tone and its harmonics would then be 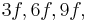3f, 6f, 9f, etc. When both tones are sounded, there are components with frequencies of 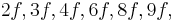2f, 3f, 4f, 6f, 8f, 9f, etc. The missing fundamental is heard because so many of these components refer to it.

The specific phenomenon that Tartini discovered was physical. Sum and difference tones are thought to be caused sometimes by the non-linearity of the inner ear. This causes intermodulation distortion of the various frequencies which enter the ear. They are combined linearly, generating relatively faint components with frequencies equal to the sums and differences of whole multiples of the original frequencies. Any components which are heard are usually lower, with the most commonly heard frequency being just the difference tone, 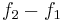f_2-f_1, though this may be a consequence of the other phenomena. Although much less common, the following frequencies may also be heard:

2f_1 - f_2, 3f_1 - 2f_2, ..., f_1 - k(f_2 - f_1)

For a time it was thought that the inner ear was solely responsible whenever a sum or difference tone was heard. However, experiments show evidence that even when using headphones providing a single pure tone to each ear separately, listeners may still hear a difference tone. Since the peculiar, non-linear physics of the ear doesn't come into play in this case, it is thought that this must be a separate, neural phenomenon. Compare binaural beats.

Heinz Bohlen proposed what is now known as the Bohlen–Pierce scale on the basis of combination tones.[2]

Contents

See also

References

  1. ^ Beament, James (2001). How We Hear Music, . The Boydell Press. ISBN 0-85115-813-7.
  2. ^ Max V. Mathews and John R. Pierce (1989). "The Bohlen–Pierce Scale", p.167. Current Directions in Computer Music Research, Max V. Mathews and John R. Pierce, eds. MIT Press.

Further reading

External links